Четыре способа решения задач на нахождение расстояния между скрещивающимися прямыми. Расстояние между двумя скрещивающимися прямыми Расстояние между прямыми в пространстве

Среди огромного количества стереометрических задач в учебниках геометрии, в различных сборниках задач, пособиях по подготовке в ВУЗы крайне редко встречаются задачи на нахождение расстояния между скрещивающимися прямыми. Возможно, это обусловлено как узостью их практического применения (относительно школьной программы, в отличие от "выигрышных" задач на вычисление площадей и объемов), так и сложностью данной темы.

Практика проведения ЕГЭ показывает, что многие учащиеся вообще не приступают к выполнению заданий по геометрии, входящих в экзаменационную работу. Для обеспечения успешного выполнения геометрических заданий повышенного уровня сложности необходимо развивать гибкость мышления, способность анализировать предполагаемую конфигурацию и вычленять в ней части, рассмотрение которых позволяет найти путь решения задачи.

Школьный курс предполагает изучение четырех способов решения задач на нахождение расстояния между скрещивающимися прямыми. Выбор способа обусловлен, в первую очередь, особенностями конкретной задачи, предоставленными ею возможностями для выбора, и, во вторую очередь, способностями и особенностями "пространственного мышления" конкретного учащегося. Каждый из этих способов позволяет решить самую главную часть задачи - построение отрезка, перпендикулярного обеим скрещивающимся прямым (для вычислительной же части задач деление на способы не требуется).

Основные способы решения задач на нахождение расстояния между скрещивающимися прямыми

Нахождение длины общего перпендикуляра двух скрещивающихся прямых, т.е. отрезка с концами на этих прямых и перпендикулярного каждой из этих прямых.

Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые.

Нахождение расстояния от точки, являющейся проекцией одной из скрещивающихся прямых, на перпендикулярную ей плоскость (так называемый "экран") до проекции другой прямой на ту же самую плоскость.

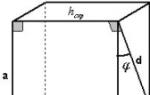
Проведем демонстрацию всех четырех способов на следующей простейшей задаче : "В кубе с ребром а найти расстояние между любым ребром и диагональю не пересекающей его грани". Ответ: .

Рисунок 1

h скр перпендикулярна плоскости боковой грани, содержащей диагональ d и перпендикулярна ребру, следовательно, h скр и является расстоянием между ребром а и диагональю d .

Рисунок 2

Плоскость A параллельна ребру и проходит через данную диагональ, следовательно, данная h скр является не только расстоянием от ребра до плоскости A, но и расстоянием от ребра до данной диагонали.

Рисунок 3

Плоскости A и B параллельны и проходят через две данные скрещивающиеся прямые, следовательно, расстояние между этими плоскостями равно расстоянию между двумя скрещивающимися прямыми.

Рисунок 4

Плоскость A перпендикулярна ребру куба. При проекции на A диагонали d данная диагональ обращается в одну из сторон основания куба. Данная h скр является расстоянием между прямой, содержащей ребро, и проекцией диагонали на плоскость C, а значит и между прямой, содержащей ребро, и диагональю.

Остановимся подробнее на применении каждого способа для изучаемых в школе многогранников.

Применение первого способа достаточно ограничено: он хорошо применяется лишь в некоторых задачах, так как достаточно сложно определить и обосновать в простейших задачах точное, а в сложных - ориентировочное местоположение общего перпендикуляра двух скрещивающихся прямых. Кроме того, при нахождении длины этого перпендикуляра в сложных задачах можно столкнуться с непреодолимыми трудностями.

Задача 1. В прямоугольном параллелепипеде с размерами a, b, h найти расстояние между боковым ребром и не пересекающейся с ним диагональю основания.

Рисунок 5

Пусть AHBD. Так как А 1 А перпендикулярна плоскости АВСD , то А 1 А AH.

AH перпендикулярна обеим из двух скрещивающихся прямых, следовательно AH?- расстояние между прямыми А 1 А и BD. В прямоугольном треугольнике ABD, зная длины катетов AB и AD, находим высоту AH, используя формулы для вычисления площади прямоугольного треугольника. Ответ:

Задача 2. В правильной 4-угольной пирамиде с боковым ребром L и стороной основания a найти расстояние между апофемой и стороной основания, пересекающей боковую грань, содержащую эту апофему.

Рисунок 6

SHCD как апофема, ADCD, так как ABCD - квадрат. Следовательно, DH - расстояние между прямыми SH и AD. DH равно половине стороны CD. Ответ:

Применение этого способа также ограничено в связи с тем, что если можно быстро построить (или найти уже готовую) проходящую через одну из скрещивающихся прямых плоскость, параллельную другой прямой, то затем построение перпендикуляра из любой точки второй прямой к этой плоскости (внутри многогранника) вызывает трудности. Однако в несложных задачах, где построение (или отыскивание) указанного перпендикуляра трудностей не вызывает, данный способ является самым быстрым и легким, и поэтому доступен.

Задача 2. Решение уже указанной выше задачи данным способом особых трудностей не вызывает.

Рисунок 7

Плоскость EFM параллельна прямой AD, т. к AD || EF. Прямая MF лежит в этой плоскости, следовательно, расстояние между прямой AD и плоскостью EFM равно расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO, следовательно, OH(EFM), следовательно, OH - расстояние между прямой AD и плоскостью EFM, а значит, и расстояние между прямой AD и прямой MF. Находим OH из треугольника AOD.

Задача 3. В прямоугольном параллелепипеде с размерами a,b и h найти расстояние между боковым ребром и не пересекающейся с ним диагональю параллелепипеда.

Рисунок 8

Прямая AA 1 параллельна плоскости BB 1 D 1 D, B 1 D принадлежит этой плоскости, следовательно расстояние от AA 1 до плоскости BB 1 D 1 D равно расстоянию между прямыми AA 1 и B 1 D. Проведем AHBD. Также, AH B 1 B, следовательно AH(BB 1 D 1 D), следовательно AHB 1 D, т. е. AH - искомое расстояние. Находим AH из прямоугольного треугольника ABD.

Ответ:

Задача 4. В правильной шестиугольной призме A:F 1 c высотой h и стороной основания a найти расстояние между прямыми:

Рисунок 9 Рисунок 10

а) AA 1 и ED 1 .

Рассмотрим плоскость E 1 EDD 1 . A 1 E 1 EE 1 , A 1 E 1 E 1 D 1 , следовательно

A 1 E 1 (E 1 EDD 1). Также A 1 E 1 AA 1 . Следовательно, A 1 E 1 является расстоянием от прямой AA 1 до плоскости E 1 EDD 1 . ED 1 (E 1 EDD 1)., следовательно AE 1 - расстояние от прямой AA 1 до прямой ED 1 . Находим A 1 E 1 из треугольника F 1 A 1 E 1 по теореме косинусов. Ответ:

б) AF и диагональю BE 1 .

Проведем из точки F прямую FH перпендикулярно BE. EE 1 FH, FHBE, следовательно FH(BEE 1 B 1), следовательно FH является расстоянием между прямой AF и (BEE 1 B 1), а значит и расстоянием между прямой AF и диагональю BE 1 . Ответ:

СПОСОБ III

Применение этого способа крайне ограничено, так как плоскость, параллельную одной из прямых (способ II) строить легче, чем две параллельные плоскости, однако способ III можно использовать в призмах, если скрещивающиеся прямые принадлежат параллельным граням, а также в тех случаях, когда в многограннике несложно построить параллельные сечения, содержащие заданные прямые.

Задача 4.

Рисунок 11

а) Плоскости BAA 1 B 1 и DEE 1 D 1 параллельны, так как AB || ED и AA 1 || EE 1 . ED 1 DEE 1 D 1 , AA 1 (BAA 1 B 1), следовательно, расстояние между прямыми AA 1 и ED 1 равно расстоянию между плоскостями BAA 1 B 1 и DEE 1 D 1 . A 1 E 1 AA 1 , A 1 E 1 A 1 B 1 , следовательно, A 1 E 1 BAA 1 B 1 . Аналогично доказываем, что A 1 E 1 (DEE 1 D 1). Т.о., A 1 E 1 является расстоянием между плоскостями BAA 1 B 1 и DEE 1 D 1 , а значит, и между прямыми AA 1 и ED 1 . Находим A 1 E 1 из треугольника A 1 F 1 E 1 , который является равнобедренным с углом A 1 F 1 E 1 , равным . Ответ:

Рисунок 12

б) Расстояние между AF и диагональю BE 1 находится аналогично.

Задача 5. В кубе с ребром а найти расстояние между двумя непересекающимися диагоналями двух смежных граней.

Данная задача рассматривается как классическая в некоторых пособиях, но, как правило, ее решение дается способом IV, однако является вполне доступной для решения с помощью способа III.

Рисунок 13

Некоторую трудность в данной задаче вызывает доказательство перпендикулярности диагонали A 1 C обеим параллельным плоскостям (AB 1 D 1 || BC 1 D). B 1 CBC 1 и BC 1 A 1 B 1 , следовательно, прямая BC 1 перпендикулярна плоскости A 1 B 1 C, и следовательно, BC 1 A 1 C. Также, A 1 CBD. Следовательно, прямая A 1 C перпендикулярна плоскости BC 1 D. Вычислительная же часть задачи особых трудностей не вызывает, так как h скр = EF находится как разность между диагональю куба и высотами двух одинаковых правильных пирамид A 1 AB 1 D 1 и CC 1 BD.

СПОСОБ IV.

Данный способ имеет достаточно широкое применение. Для задач средней и повышенной трудности его можно считать основным. Нет необходимости применять его только тогда, когда один из трех предыдущих способов работает проще и быстрее, так как в таких случаях способ IV может только усложнить решение задачи, или сделать его труднодоступным. Данный способ очень выгодно использовать в случае перпендикулярности скрещивающихся прямых, так как нет необходимости построения проекции одной из прямых на "экран"

L и стороной основания a .

Рисунок 16

В данной и аналогичных ей задачах способ IV быстрее других способов приводит к решению, так как построив сечение, играющее роль "экрана", перпендикулярно AC (треугольник BDM), видно, что далее нет необходимости строить проекцию другой прямой (BM) на этот экран. DH - искомое расстояние. DH находим из треугольника MDB, используя формулы площади. Ответ: .

В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).

Для нахождения расстояния между скрещивающимися прямыми необходимо:

1. Провести через одну из скрещивающихся прямых плоскость, которая параллельна другой скрещивающейся прямой.
2. Опустить перпендикуляр из любой точки второй прямой на полученную плоскость. Длина этого перпендикуляра будет являться искомым расстоянием между прямыми.

Разберем данный алгоритм подробнее на примере решения задачи C2 из ЕГЭ по математике.

Расстояние между прямыми в пространстве

Задача. В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние между прямыми BA 1 и DB 1 .

Рис. 1. Чертеж к задаче

Решение. Через середину диагонали куба DB 1 (точку O ) проведем прямую, параллельную прямой A 1 B . Точки пересечения данной прямой с ребрами BC и A 1 D 1 обозначаем соответственно N и M . Прямая MN лежит в плоскости MNB 1 и параллельна прямой A 1 B , которая в этой плоскости не лежит. Это означает, что прямая A 1 B параллельна плоскости MNB 1 по признаку параллельности прямой и плоскости (рис. 2).

Рис. 2. Искомое расстояние между скрещивающимися прямыми равно расстоянию от любой точки выделенной прямой до изображенной плоскости

Ищем теперь расстояние от какой-нибудь точки прямой A 1 B до плоскости MNB 1 . Это расстояние по определению будет являться искомым расстоянием между скрещивающимися прямыми.

Для нахождения этого расстояния воспользуемся методом координат. Введем прямоугольную декартову систему координат таким образом, чтобы ее начало совпало с точкой B, ось X была направлена вдоль ребра BA , ось Y — вдоль ребра BC , ось Z — вдоль ребра BB 1 (рис. 3).

Рис. 3. Прямоугольную декартову систему координат выберем так, как показано на рисунке

Находим уравнение плоскости MNB 1 в данной системе координат. Для этого определяем сперва координаты точек M , N и B 1: Полученные координаты подставляем в общее уравнение прямой и получаем следующую систему уравнений:

Из второго уравнения системы получаем из третьего получаем после чего из первого получаем Подставляем полученные значения в общее уравнение прямой:

Замечаем, что иначе плоскость MNB 1 проходила бы через начало координат. Делим обе части этого уравнения на и получаем:

Расстояние от точки до плоскости определяется по формуле.

РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Расстоянием между двумя скрещивающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым. Если одна из двух скрещивающихся прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью. Если две скрещивающиеся прямые лежат в параллельных плоскостях, то расстояние между этими прямыми равно расстоянию между параллельными плоскостями.

Куб 1 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и BC. Ответ: 1.

Куб 2 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и CD. Ответ: 1.

Куб 3 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и B 1 C 1. Ответ: 1.

Куб 4 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и C 1 D 1. Ответ: 1.

Куб 5 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и BC 1. Ответ: 1.

Куб 6 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и B 1 C. Ответ: 1.

Куб 7 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и CD 1. Ответ: 1.

Куб 8 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и DC 1. Ответ: 1.

Куб 9 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и CC 1. Ответ:

Куб 10 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и BD. Решение. Пусть O – середина BD. Искомым расстоянием является длина отрезка AO. Она равна Ответ:

Куб 11 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и B 1 D 1. Ответ:

Куб 12 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и BD 1. Решение. Пусть P, Q – середины AA 1, BD 1. Искомым расстоянием является длина отрезка PQ. Она равна Ответ:

Куб 13 В единичном кубе A…D 1 найдите расстояние между прямыми AA 1 и BD 1. Ответ:

Куб 14 В единичном кубе A…D 1 найдите расстояние прямыми AB 1 и CD 1. Ответ: 1.

Куб 15 В единичном кубе A…D 1 найдите расстояние между прямыми AB 1 и BC 1. Решение. Искомое расстояние равно расстоянию между параллельными плоскостями AB 1 D 1 и BDC 1. Диагональ A 1 C перпендикулярна этим плоскостям и делится в точках пересечения на три равные части. Следовательно, искомое расстояние равно длине отрезка EF и равно Ответ:

Куб 16 В единичном кубе A…D 1 найдите расстояние между прямыми AB 1 и A 1 C 1. Решение аналогично предыдущему. Ответ:

Куб 17 В единичном кубе A…D 1 найдите расстояние между прямыми AB 1 и BD. Решение аналогично предыдущему. Ответ:

Куб 18 В единичном кубе A…D 1 найдите расстояние прямыми AB 1 и BD 1. Решение. Диагональ BD 1 перпендикулярна плоскости равностороннего треугольника ACB 1 и пересекает его в центре P вписанной в него окружности. Искомое расстояние равно радиусу OP этой окружности. OP = Ответ:

Пирамида 1 В единичном тетраэдре ABCD найдите расстояние между прямыми AD и BC. Решение. Искомое расстояние равно длине отрезка EF, где E, F – середины ребер AD, GF. В треугольнике DAG DA = 1, AG = DG = Ответ: Следовательно, EF =

Пирамида 2 В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми AB и CD. Ответ: 1.

Пирамида 3 В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BD. Решение. Искомое расстояние равно высоте OH треугольника SAO, где O – середина BD. В прямоугольном треугольнике SAO имеем: SA = 1, AO = SO = Ответ: Следовательно, OH =

Пирамида 4 В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC. Решение. Плоскость SAD параллельна прямой BC. Следовательно, искомое расстояние равно расстоянию между прямой BC и плоскостью SAD. Оно равно высоте EH треугольника SEF, где E, F – середины ребер BC, AD. В треугольнике SEF имеем: EF = 1, SE = SF = Высота SO равна Следовательно, EH = Ответ:

Пирамида 5 В правильной 6 -ой пирамиде SABCDEF, ребра основания которой равны 1, найдите расстояние между прямыми AB и DE. Ответ:

Пирамида 6 В правильной 6 -ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние между прямыми SA и BC. Решение: Продолжим ребра BC и AF до пересечения в точке G. Общим перпендикуляром к SA и BC будет высота AH треугольника ABG. Она равна Ответ:

Пирамида 7 В правильной 6 -ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние между прямыми SA и BF. Решение: Искомым расстоянием является высота GH треугольника SAG, где G – точка пересечения BF и AD. В треугольнике SAG имеем: SA = 2, AG = 0, 5, высота SO равна Отсюда находим GH = Ответ:

Пирамида 8 В правильной 6 -ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние между прямыми SA и CE. Решение: Искомым расстоянием является высота GH треугольника SAG, где G – точка пересечения CE и AD. В треугольнике SAG имеем: SA = 2, AG = , высота SO равна Отсюда находим GH = Ответ:

Пирамида 9 В правильной 6 -ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние между прямыми SA и BD. Решение: Прямая BD параллельна плоскости SAE. Искомое расстояние равно расстоянию между прямой BD и этой плоскостью и равно высоте PH треугольника SPQ. В этом треугольнике высота SO равна, PQ = 1, SP = SQ = Отсюда находим PH = Ответ:

Пирамида 10 В правильной 6 -ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние между прямыми SA и BG, где G – середина ребра SC. Решение: Через точку G проведем прямую, параллельную SA. Обозначим Q точку ее пересечения с прямой AC. Искомое расстояние равно высоте QH прямоугольного треугольника ASQ, в котором AS = 2, AQ = , SQ = Отсюда находим QH = Ответ: .

Призма 1 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: BC и B 1 C 1. Ответ: 1.

Призма 2 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC. Ответ:

Призма 3 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1. Ответ:

Призма 4 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 C 1. Ответ: 1.

Призма 5 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 C. Решение: Искомое расстояние равно расстоянию между прямой AB и плоскостью A 1 B 1 C. Обозначим D и D 1 середины ребер AB и A 1 B 1. В прямоугольном треугольнике CDD 1 из вершины D проведем высоту DE. Она и будет искомым расстоянием. Имеем, DD 1 = 1, CD = Ответ: Следовательно, DE = , CD 1 = .

Призма 6 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BC 1. Решение: Достроим призму до 4 -х угольной призмы. Искомое расстояние будет равно расстоянию между параллельными плоскостями AB 1 D 1 и BDC 1. Оно равно высоте OH прямоугольного треугольника AOO 1, в котором Ответ. Эта высота равна

Призма 7 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 B 1. Ответ: 1.

Призма 8 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и B 1 C 1. Ответ: 1.

Призма 9 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и C 1 D 1. Ответ: 1.

Призма 10 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и DE. Ответ: .

Призма 11 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB и D 1 E 1. Ответ: 2.

Призма 12 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CC 1. Ответ: .

Призма 13 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DD 1. Ответ: 2.

Призма 14 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и B 1 C 1. Решение: Продолжим стороны B 1 C 1 и A 1 F 1 до пересечения в точке G. Треугольник A 1 B 1 G равносторонний. Его высота A 1 H является искомым общим перпендикуляром. Его длина равна. Ответ: .

Призма 15 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и C 1 D 1. Решение: Искомым общим перпендикуляром является отрезок A 1 C 1. Его длина равна. Ответ: .

Призма 16 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1. Решение: Искомым расстоянием является расстояние между параллельными плоскостями ADD 1 и BCC 1. Оно равно. Ответ: .

Призма 17 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CD 1. Решение: Искомым общим перпендикуляром является отрезок AC. Его длина равна. Ответ: .

Призма 18 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DE 1. Решение: Искомым общим перпендикуляром является отрезок A 1 E 1. Его длина равна. Ответ: .

Призма 19 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BD 1. Решение: Искомым общим перпендикуляром является отрезок AB. Его длина равна 1. Ответ: 1.

Призма 20 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CE 1. Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CEE 1. Оно равно. Ответ: .

Призма 21 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BE 1. Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью BEE 1. Оно равно. Ответ: .

Призма 22 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CF 1. Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CFF 1. Оно равно. Ответ: .

Призма 23 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите угол между прямыми: AB 1 и DE 1. Решение: Искомым расстоянием является расстояние между параллельными плоскостями ABB 1 и DEE 1. Расстояние между ними равно. Ответ: .

Призма 24 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите угол между прямыми: AB 1 и CF 1. Решение: Искомым расстоянием является расстояние между прямой AB 1 и плоскостью CFF 1. Оно равно. Ответ:

Призма 25 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BC 1. Решение: Пусть O, O 1 –центры граней призмы. Плоскости AB 1 O 1 и BC 1 O параллельны. Плоскость ACC 1 A 1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG 1 и GC 1. В параллелограмме AGC 1 G 1 имеем AG = Ответ: ; AG 1 = Высота, проведенная к стороне AA 1 равна 1. Следовательно, d= . .

Призма 26 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BD 1. Решение: Рассмотрим плоскость A 1 B 1 HG, перпендикулярную BD 1. Ортогональная проекция на эту плоскость переводит прямую BD 1 в точку H, а прямую AB 1 – в прямую GB 1. Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB 1. В прямоугольном треугольнике GHB 1 имеем GH = 1; Ответ: B 1 H = . Следовательно, d = .

Призма 27 В правильной 6 -й призме A…F 1, ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BE 1. Решение: Рассмотрим плоскость A 1 BDE 1, перпендикулярную AB 1. Ортогональная проекция на эту плоскость переводит прямую AB 1 в точку G, а прямую BE 1 оставляет на месте. Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE 1. В прямоугольном треугольнике A 1 BE 1 имеем A 1 B = ; A 1 E 1 =. Ответ: Следовательно, d = .

«Расстояние между скрещивающимися прямыми» - Теорема. Подготовительные устные задачи. Найдите расстояние между прямой MN и плоскостью AA1D1D. Найдите расстояние между прямой B1K и плоскостью DD1C1C. OK=OO1?OM/O1M =a/3 (по теореме Пифагора O1M=3/2?2, OM=1/2?2). Диагональная плоскость AA1C1C перпендикулярна прямой BD. Новые положения точек B и N будут ближайшими друг к другу точками прямых AD и BM.

«Урок Скорость время расстояние» - Математическая разминка. Цель урока: научить учащихся решать задачи на движение. Расстояние. За какое время можно пройти 30 км с постоянной скоростью 5 км/ч? Взаимосвязь между скоростью, временем и расстоянием. Сколько человек шло в город? Самолет пролетает расстояние от города А до города В за 1 ч. 20 мин.

«Скорость время расстояние математика» - Сумму чисел 5 и 65 уменьшить в 2раза. Незнайка отправился на Луну. Путешествие по страницам сказочной книги. Физкультминутка. Один вышел в 8 часов, а другой – в 10 часов. Подведение итогов. Права ли Лора? -Лора задачу такую решила: «500 км. проедет машина За 10 часов. Время. Ключ с ответом «38» открывает книгу:

«Диалог прямая речь» - Чем отличается прямая речь от диалога? Например: Л. Н. Толстой сказал: «Все мы на свете друг другу нужны». Графика прямой речи. А: «п.». Задание 3. Заменить прямую речь диалогом. Например: «П?» - а. «П!» - а. Укажите правильные схемы к следующим предложениям. Графика диалога. Как на письме оформить прямую речь и диалог?

«Предложения с прямой речью» - Петроний, древнеримский писатель. Игра «Найди ошибку» (проверка). Авторские слова, вводящие прямую речь: Я пов..новался и пошёл в дом отца Герасима. Ко мне приехала в гости подруга из деревни. Предложения с прямой речью. Творческое задание. На письме прямая речь заключается в кавычки. Читайте!» - восклицал Константин Георгиевич Паустовский.

«Расстояние и масштаб» - Модель атома в высоком масштабе увеличения. На карте с масштабом расстояние равно 5 см. Если масштаб задан дробью с числителем 1, то. Модель пожарной машины в уменьшенном масштабе. Алгоритм нахождения расстояния на местности: По автотрассе протяженность маршрута 700 км. Закончите фразу: Расстояние между двумя городами равно 400 км.